강의보고오기: https://youtu.be/GUKp4LZiovQ?si=FdianS1OlGKp6_dn
이번 강의 내용은 Direct Solution입니다.
핵심내용
복잡한 수학을 알려드릴건데 다 아실 필요는 없습니다. 기억해야 할 거 먼저 말씀드리겠습니다.
Direct Solution은 컴퓨팅 비용이 높아서 빨간선을 구하기 위한 알고리즘으로 Gradient Descet를 쓴다는 것입니다.
독립변수가 d개여도 선형관계이다.
위 밑줄 친 내용을 알기위해 다소 어려운 수학 얘기를 할 것입니다. 읽고 싶은 분만 읽어주세요 ^^.
우리가 선형회귀를 모델을 배우기 전에 익숙했던 $ y = ax + b $ 에서 우리의 관심은 $x, y$ 값 자체였습니다. 하지만 머신러닝에서 $x, y$는 데이터로서 주어지는 값이고 우리는 데이터의 의미를 찾아내기 위하여 선형회귀를 활용하여 $a, b$를 찾는것 입니다.
$x$ 독립변수는 여러 개일 수 있습니다. 지난 강의에도 말씀드렸듯이, 집값($y$)에 영향을 미치는 요소는 여러가지가 있을 수 있겠죠? 그 식을 일반화 하면 아래와 같이 나타낼 수 있는 거죠.
$$ \hat{y}(x;w) = w_0 + w_1x_1 + ... + w_dx_d = w^Tx, \quad \text{where} \\
x = \begin{bmatrix}
1 \ x_1 \ x_2 \ ... \ x_d
\end{bmatrix}^T, \quad w = \begin{bmatrix}
w_0 \ w_1 \ w_2 \ ... \ w_d
\end{bmatrix}^T$$
강의예제: 독립변수 2개
강의에서 사용한 예제는 다음과 같습니다.
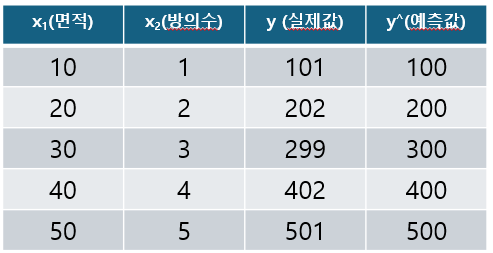
이 예제에 대한 회귀식을 나타내면 $ \hat{y}(x;w) = w_0 + w_1x_1 + w_2x_2 = w^Tx $ 입니다. 우리는 $w$를 구해야 합니다. 어떻게 구할까요?
네 맞습니다. 지난 강의에서 $w$를 구하기 위해 MSE, SSE를 쓴다고 말씀드렸습니다.
1. SSE: $$ L(w) = \sum_{i=1}^N (w^Tx_i - y_i)^2 $$
2. MSE: $$ L(w) = \frac{1}{N}\sum_{i=1}^N (w^Tx_{i} - y_{i})^{2} $$
그런데 예제를 자세히 보시면 데이터 한줄이 $ \hat{y}(x;w) = w_0 + w_1x_1 + w_2x_2 = w^Tx $ 이 식에 대응되는 거라는 것을 알 수 있습니다. 그래서 데이터 전체를 한번에 계산하기 위해서 벡터 곱셈이 아니라 데이터에 대한 행렬식을 사용할 수 있습니다. 행렬식으로 나타내면,
$$ L(w) = \frac{1}{N} \lVert Xw - Y \rVert^2 $$ 이 됩니다.
(행렬, 벡터식에서 대문자이면 행렬, 소문자이면 벡터를 의미합니다.)
위 행렬로 표현한 식을 예제와 연결해보겠습니다. 사실 별거 아닙니다.
$$ \begin{bmatrix}
1 & 10 & 1 \\
1 & 20 & 2 \\
1 & 30 & 3 \\
1 & 40 & 4 \\
1 & 50 & 5
\end{bmatrix}
\begin{bmatrix}
w_0 \\
w_1 \\
w_2
\end{bmatrix} -
\begin{bmatrix}
101 \\
202 \\
209 \\
402 \\
501
\end{bmatrix} $$
첫번째가 $X$ 행렬입니다. 첫번째 열은 $w_0$와 곱해지기 위해 1로 통일합니다. bias에 대한 값이죠. 두 번째 열은 집의 면적, 3번째 열은 방의 수에 대한 데이터 입니다. 두 번째는 $w$ 벡터이고 세 번째는 당연히 실제 $y$ 값, 즉 데이터 상에서 실제 집값을 의미합니다.
강의에서 이 식을 통해 $w$ 벡터를 구하는 과정을 설명했습니다. 과정에서 $w$벡터에 대한 미분을 합니다. 벡터를 미분하는게 처음이신 분들도 있을겁니다. 이번 강에서는 벡터를 미분하는 방법만 설명합니다. 벡터미분에 대한 자세한 내용은 다음강에서 다룰 예정입니다. 꼭 알아야 하는 내용은 아니지만, 아신다면 앞으로 많은 부분에서 이해가 편하실 겁니다. Gradient도 스칼라 값을 벡터로 미분한 결과거든요. 또한, 딥러닝의 깊은 이해를 위해서는 필수적으로 아셔야 합니다.
Direct Solution
마지막으로, 미분식이 '0'이 될때 최소값이니까 미분식에 0을 대입해서 값을 구하면, 아래와 같은 값이 나옵니다.
$$ w = (X^TX)^{-1}X^TY $$
위와 같이 구하는 방법을 Direct Solution이라고 합니다. Direct Solution은 최소 제곱법(OLS)을 사용하여 선형 회귀 모델의 파라미터를 직접 계산하는 알고리즘입니다.
컴퓨터로 $w$를 위 계산으로 구할 수 있을까요? 네 당연히 구할 수 있습니다. 하지만, 우리는 python 코딩을 할때 저 계산을 사용하지 않습니다. Tensorflow 등 머신러닝관련 패키지 내에 알고리즘도 당연히 Direct Solution을 사용하지 않습니다.
Direct Solution을 쓰지 않는 이유
Direct Solution으로 구할 수 있고, 코딩에서 Direct Solution을 바로 쓰는 것도 꽤 간편하고 괜찮아 보이는데 왜 사용하지 않을까요?
컴퓨팅 비용이 매우 높기 때문입니다. 저기 보이는 역행렬 연산이 끝내주게 힘듭니다. 우리 예제는 겨우 데이터 5줄짜리 였지만 실제 데이터는 독립변수가 더 많고 데이터도 5개 보다 훨씬 많을 겁니다.
혹시 3차원 행렬에 대한 역행렬 계산 직접 해보셨나요? 3차원만 해봐도 상당히 힘듭니다. 노가다가 상당하죠. 컴퓨터도 마찬가지입니다. 역행렬 연산은 $O(d^3)$의 복잡도입니다. 그래서 이 Direct Solution을 사용하지 않는 겁니다.
물론 지금 좋은 GPU를 가진 컴퓨터가 있다면 사실 Direct solution을 써도 상관없이 빨리 될겁니다.
GPU면 왜 빠르냐고요?
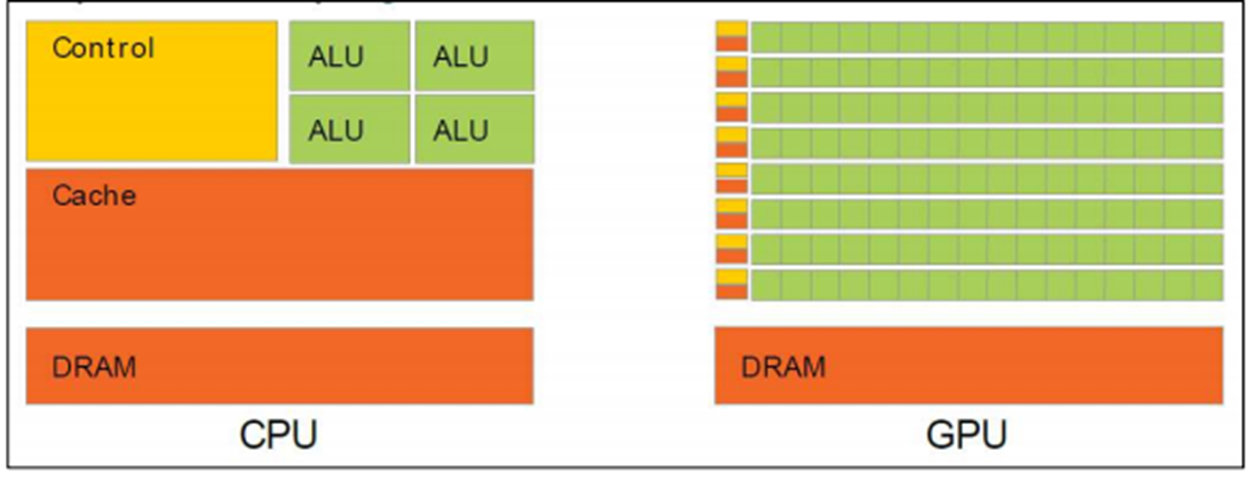
위 그림은 CPU와 GPU의 차이입니다. GPU가 계산할 수 유닛인 ALU가 훨씬 많죠? 행렬연산 잘 생각해보면 아주 단순한 연산의 반복이죠? 첫번째 행렬의 행과 두번째 행렬의 열을 차례로 곱해가면서 연산하는거죠. GPU는 이 연산을 병렬로 수행합니다. 병렬로 수행해서 금방 다 더해버립니다. CPU 및 저와 다르게 Multi Taking 능력이 최상급입니다.
근데 선형회귀를 처음 발견할 시기에 이렇게 병렬연산을 할 수 있는 GPU가 있었을까요? 없었겠죠? 그리고 다른 방법이 있는데 굳이 비싼 GPU를 쓰는 연산을 할 필요도 없죠.
다른 방법이 뭐냐고요?
앞에서 말씀드린 Gradient Descent입니다. 사실 이 강의에서 기억해야 하는 것 중 가장 중요한 겁니다. Direct Solution은 컴퓨팅 비용이 높아서 빨간선을 구하기 위한 알고리즘으로 Gradient Descet를 쓴다는 것입니다.
다음 강에서는 이번 강에서 사용한 벡터미분에 대해서 다루도록 하겠습니다.
'Machine Learning' 카테고리의 다른 글
| 11강 그래디언트(그라디언트의 뜻, 방향, 크기) (0) | 2024.07.25 |
|---|---|
| 10강 벡터미분(Feat. Jacobian & Hessian) (1) | 2024.07.22 |
| 8강 선형회귀 - Loss Function (0) | 2024.07.20 |
| 7강 벡터 (0) | 2024.07.20 |
| 6강 선형회귀 (0) | 2024.07.18 |