지난 시간 정리
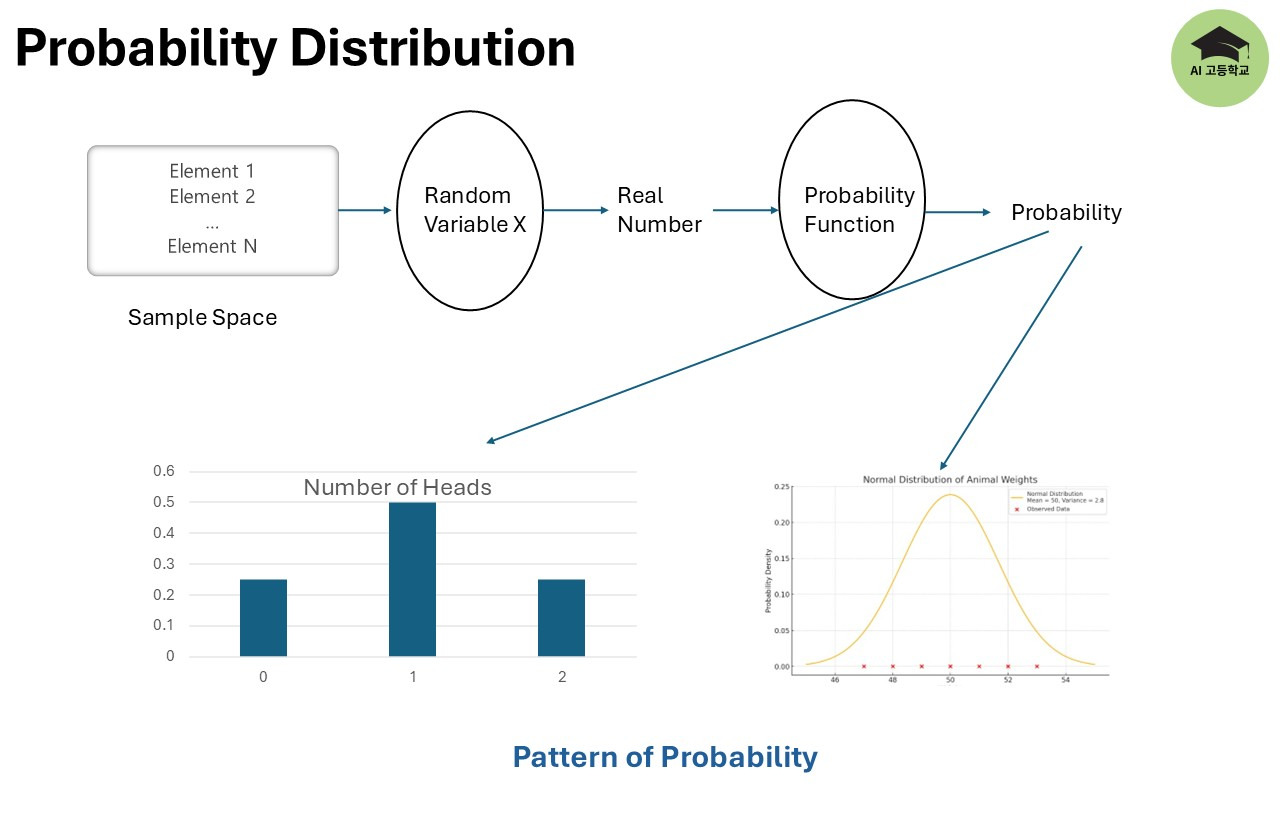
지난 시간에 표본공간, 실험, 사건, 확률변수, 확률함수 등을 정리했습니다. 중요하게 기억해야 할 것은 확률변수입니다.
확률변수는 표본공간의 원소를 실수로 변환하는 함수입니다.
- 동전을 던져 앞면을 1, 뒷면을 0으로 변환한다고 가정하면, 확률변수 𝑋는 다음과 같이 정의됩니다:
𝑋(𝐻) = 1, 𝑋(𝑇)= 0 - 즉, 표본공간 {𝐻,𝑇}를 실수 {1,0}으로 변환하는 역할을 합니다.
또한 확률함수는 확률변수의 값을 확률로 변환하는 함수라는 것입니다. 그리고 이 확률함수는 이산형확률함수와 연속형확률함수로 나눌 수 있고, 이 두개의 이름이 다릅니다. 이산형확률함수를 확률질량함수라고 하고, 연속형확률함수를 확률밀도함수라고 합니다.
강의보러가기: https://youtu.be/lvka0j2_7ic?si=DC0ggGwEt_oj77wK
이산형확률변수
Bernoulli Distribution
확률변수로 성공은 1 실패는 0으로 변환하고 성공의 확률을 $p$ 라고 두면 확률 함수는 아래와 같습니다.
$$ f_X(x;p) = p^x(1-p)^{1-x}, \space\space x = 0\space or \space1 $$
$ f_X(x;p) $는 $p$로 Parameterized 된 확률변수 X에 대한 x확률변수 함수라는 뜻입니다. $p$로 parameterized 됐다는 건 p에 의해 확률분포 모양이 변한다는 의미입니다.
아주 쉽습니다. 한 번 시도이니까 만약 성공이면 $ x = 1 $ 이니까 $p$가 되고 실패라면 x = 0 이니까 $1-p$가 됩니다. 베르누이라는 말에 어려움을 느끼지만, 제일 쉽습니다.
평균과 분산
$$ E[X] = p $$
$$ V[X] = p(1 - p) $$
위 식은 따로 설명할 필요없을 것 같습니다. 성공 확률이 p니까 평균적으로 p의 확률만큼 성공하겠죠. 분산은 성공확률 $p$를 중심으로 $1-p$만큼 퍼져있는겁니다. 수학식으로는 아래와 같이 됩니다.
$$ E[X] = \sum_{x=0,1} xp^x(1-p)^{1-x} = 0 + p = p$$
$$ V[X] = E[X^2] - (E[x])^2 = \sum_{x=0,1} x^2p^x(1-p)^{1-x} = p - p^2 = p(1-p)$$
강의에서 $ V[X] = E[X^2] - (E[x])^2 = \sum_{x=0,1} x^2p^{x^2}(1-p)^{1-x^2} $이라고 썼는데 강의내용이 틀렸으니 참고하시기 바랍니다. 글이 수정이 쉬워서 글먼저 쓰고 유트브를 만드는게 더 품질이 좋을 것 같은데, 블로그 글쓰기는 저도 모르게 계속 미루게 됩니다.
Binomial Distribution
베루누이분포와 거의 똑같습니다. 다만 시행을 여러번 즉, n번한다고 가정하고 확률변수는 성공의 횟수로 합니다. 그래서 아래와 같은 확률질량함수가 나옵니다.
$$ f_X(x;p) = \binom{n}{x}p^x(1-p)^{1-x} \space \space, for x = 0, \space1, \space\space...,n$$
이 전에 설명을 해서 설명은 생략합니다.
평균과 분산
$$ E[X] = np $$
$$ V[X] = np(1 - p) $$
1번 일때는 p이고 n번 시행하니까 평균이 np가 됩니다. 자세한 설명은 생략하겠습니다.
연속형확률변수
연속형확률변수는 특정값으로 나타내지 않고 범위로 나타냅니다. 왜냐하면 연속형확률함수의 확률밀도함수는 범위를 확률로 변환해줍니다. 연속형확률함수의 특정값에서의 확률은 항상 0입니다.
연속형확률변수의 특징을 보겠습니다.
1. Uncountable
연속형확률변수는 Uncoutable입니다. 우리 정규분포의 MLE를 공부하며 동물의 몸무게 예시를 봤었습니다. 동물의 무게를 셀 수 있을까요? 무게가 정확히 같은 동물은 없을 겁니다. 0.0000000000000000000000000000000000000000000001 그램이라도 다르겠죠.
2. Range
셀 수 없기때문에 범위로 표시합니다. $[0, 1]$은 0과 1사이의 범위를 의미하고 0과 1을 포함합니다. $(0, 1]$ 0과 1사이의 범위를 의미하고 0은 포함하지 않고 1은 포함합니다.
3. $ \int $
$\sum$ 대신 $\int$를 활용합니다. 네, 범위를 적분하고 적분한 값이 확률을 의미합니다. 적분을 사용하니까 특정값에서 적분은 0이 되는 겁니다. $\int^{a}_{a} f(x)dx$ 는 항상 0입니다.
확률밀도함수
$$ P=(a\leq X \leq b) = \int^{a}_{b} f(x) dx $$
위 식에서 볼 수 있듯이 확률변수 X가 a와 b사이에 있을 확률은 오른쪽 식이 됩니다. f(x)가 확률밀도함수이고, 적분하여 확률을 구합니다. 적분되는 식 $f(x)$가 확률밀도함수입니다.
확률질량함수와 범위를 보는관점이 다릅니다. 확률질량함수에서의 확률변수는 < 와 $\leq일때 값의 차이가 있습니다. 하지만 연속형은 값이 같습니다.
예를들어 누적질량함수를 구할때 $P(a < X \leq b)$ $\neq$ $P(a < X < b) $ 와 같이 범위에서 a 또는 포함되느냐 아니냐에 따라서 확률값이 달라지지만, 연속형확률변수는 $P(a < X \leq b)$ = $P(a < X < b) $ a와 b 포함여부에 관계없이 같습니다. 적분의 성질을 잘 생각보시면 됩니다.
누적밀도함수
$$F(x) = P(X \leq x) = \int^{x}_{-\infty} f(t) dt $$
입니다. 확률밀도함수를 적분하면 누적밀도함수가 됩니다. 당연히 누적밀도함수를 미분하면 확률밀도함수가 됩니다.
평균과 분산
$$E[x] = \int xf(x) dx $$
$$V[x] = E[(x-\mu)^2] = E[X^2] - (E[X])^2 $$
상세한 내용은 강의를 참고하시 바랍니다.
'Machine Learning' 카테고리의 다른 글
| 20강 [확률과 통계 1부] 확률변수/확률함수/확률분포 (0) | 2024.11.24 |
|---|---|
| 19강 [MLE 5부] 가우시안 분포(정규분포) 데이터의 MLE (0) | 2024.09.01 |
| 18강 [최대우도추정법, MLE 4부] MLE 완전정복, Log Likelihood의 이해 (4) | 2024.09.01 |
| 17강 [최대우도추정법, MLE 3부] 로또확률 및 이항분포 (0) | 2024.08.31 |
| 16강 [최대우도추정법, MLE 2부] Bayes 정리에 있는 우도와 MLE 소개 (0) | 2024.08.24 |